Advanced use of hash codes in Java: duplicate elimination with a BitSet

On the previous page, we introduced the problem of duplicate elimination when we had a fairly large number of elements: for example, writing some data to a database table for a given client only if we hadn't previously logged the data for that client's IP address. A possible solution, but a memory- and object-hungry one, was to store a the previously-seen IP addresses as strings, or better their hash codes. in a HashSet. On this page, we'll consider that a more efficient structure could be a BitSet.

Now let's think again about the statistics of hash codes, and about what our actual purpose is here. For a given IP address, we only want to store a "true" or "false" value: i.e. one bit of information. Now let's suppose for a minute that we had a hash table with a million buckets but which only allowed one hash code per bucket. The process would be as follows:

have a BitSet with a million bits;
for a given item IP address, calculate the hash code;
for that hash code, calculate the bucket number n, as the hash code modulo a million (hashCode % noBuckets);
we consider that IP address to be present if the nth bit in the BitSet is set (and set it to indicate that it's present).

Now, because we're not dealing with collisions, that will mean that in some cases, we'll get some "false positives": where one IP address is incorrectly eliminated because we previously set its bit based on another IP address whose hash code modulo a million happened to result in the same bit index. But we can calculate how often we expect this to happen, and the error rate may be acceptable for the purposes of our logging.

Recall the approximation:

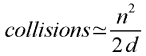
After 50,000 distinct IP addresses and a million buckets, the number of expected collisions will be approximately 50,000²/2 million, or about 1250. In other words, we will incorrectly discard about 1 in 50 clients because we think we've already logged them. For our purposes, that may be an acceptable error rate. And if it's not, we can increase the number of bits to give a better error rate (doubling the number of bits roughly halves the error rate, as indicated by the formula).

A million bits is about 122K; our equivalent hash set would require in the order of a couple of megabytes and the creation of tens of thousands of objects! As the number of distinct items increases, this technique could be the difference between storing the set in memory and having to hit the database every time...!

What do you think of this article? Did it help you? Found a mistake? Feedback and suggestions here

Written by Neil Coffey. Copyright © Javamex UK 2010. All rights reserved. If you have any feedback on the Java collections tutorials in this section or about the content of this site in general, please leave a message on the Javamex forum.