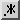
The cost of Java object orientation in mathematical calculations: creating a Newton's method fractal

Fractal image based on the equation x² - 4 = 0.

Newton's method fractals

Our goal is to create an image such as that shown opposite. Taking the simple equation:

the image gives a graphical representation of how, applying Newton's method, different starting values of x converge on a particular solution to the equation (x = -2 or x = 2), and how quickly. Essentially, we do the following:

• let the X coordinate of the image represent the real component of the starting value of x;
• let the Y coordinate of the image represent the imaginary component of the starting value of x;
• for each pixel in the image, calculate the corresponding complex number that is to be the starting value of x (we pick particular minimum and maximum values for the real and imaginary components and then map intermediate values to each pixel in the image);
• run Newton's method on that particular starting value of x and make a note of: (a) which solution (-2 or 2) comes out, and (b) how many iterations it takes to arrive at the solution;
• colour the pixel red if the solution comes out as -2, and green if it comes out as 2, and make the brightness of the pixel reflect the number of iterations needed to reach the solution.

The overall code looks as follows:

public class NewtonFractal {
  private int resX = 1280, resY = 1024;
  private int maxIter = 16;
  // Real and imaginary components of starting value of x for current pixel
  private double xr, xi;
  // Range of real and imaginary components over which we plot
  private double xrMin = -16, xrMax = 16, xiMin = -12, xiMax = 12;
  private double xrStep = (xrMax - xrMin) / resX;
  private double xiStep = (xiMax - xiMin) / resY;
  // Used to pass results of calculation back to outer method
  private double xrResult, xiResult;
  private int iter;

  public void makeFractal() {
    BufferedImage bimg = new BufferedImage(resX, resY, BufferedImage.TYPE_3BYTE_BGR);
    xi = xiMin;
    for (int y = resY-1; y >= 0; y--) {
      xr = xrMin;
      for (int x = 0; x < resX; x++) {
        iterate();
        // Calc pixel brightness and colour
        int deg = (iter < 0) ? 0 :
          ((iter >= maxIter ) ? 255 : (int) (255 * (maxIter - 1 - iter) / maxIter));
        int rgb = (xrResult > 1.9) ?
          (deg << 8) : (deg << 16);
        bimg.setRGB(x, y, rgb);
        xr += xrStep;
      }
      xi += xiStep;
    }
    try {
      ImageIO.write(bimg, "BMP", new File("Fractal.bmp"));
    } catch (IOException e) {
      throw new RuntimeException("Couldn't save!", e);
    }
  }
}

The interesting things actually happen in iterate(). This is where we take the current values of xr and xi, use them as the real and imaginary components of the starting value of x, then run Newton's method to find the solution to x² - 4 = 0 for that starting value of x. Using our complex number class from earlier, the implementation looks something as follows:

private void iterate() {
  ComplexNumber x = new ComplexNumber(this.xr, this.xi);
  iter = -1;
  for (int i = 0; i < 100; i++) {
    // x <- x - (x**2 - 4) / 2x
    ComplexNumber num = x.multiply(x).addReal(-4d);
    ComplexNumber denom = x.multiplyReal(2d);
    ComplexNumber frac = num.divide(denom);
    x = x.subtract(frac);
    if (frac.real() == 0 && frac.imaginary() == 0) {
      iter = i;
      break;
    }
  }
  this.xrResult = x.real();
  this.xiResult = x.imaginary();
}

Working through the code, you'll hopefully agree that this corresponds to applying Newton's method with x <— x - (x² - 4) / 2x on each iteration.

In reality, we could of course return a ComplexNumber object with the result, but in a moment we want to consider the case where we do away with the ComplexNumber class.

Optimisations

On the next page, we consider two optimisations to reduce the cost of object orientation, before weighing up how much of a performance gain these actually bring and whether they might be worth the codability and maintainability tradeoff that they each bring.