How the String hash function works (2)
Ironing out the bias
This page continuous from page 1 of our discussion on how the Java String hash function works.
So far, we posed a hypothetical set of random strings, where each character has
particular distribution. We found that, as is actually quite typical with
strings, characters are biased towards certain bits being set.
In our example, bits 4 and 5 had a just over 70% and 75% chance of being set
respectively for a given character. The lower bits showed better randomness:
i.e. their chance of being set was closer to 50%.
The trick of the string hash function is to try and iron out this bias
by mixing bits with a biased probability with other bits, in particular
those where the probability is already fairly unbiased.
First: a not-so-good hash function
Recall that the Java String function combines successive characters
by multiplying the current hash by 31 and then adding on the new character.
To show why this works reasonably well for typical strings, let's start by
modifying it so that we instead use the value 32 as the hash code. In other
words, let's imagine the hash function is this:
int hash = 0;
for (int i = 0; i < length(); i++) {
hash = 32 * hash + charAt(i);
}
return hash;
Note that this is a arguably bad hash function for strings1
(and possibly for most things).
The problem is that we are multiplying by a power of 2, which in effect
simply shifts the current hash along.
Some mixing then does take place: the high bits of the ith character
will be mixed with the lower bits of the previous character (now shifted left 5
places so that its lower 3 bits coincide with the upper 3 bits of the
ith character). However, this isn't enough to completely remove
the pattern of biases from the resulting hash code.
The problem can be illustrated
if we take random series of 5 characters (with the distribution we've been
discussing). The graph to the right shows the probability of each successive bit
of the hash code being set.
The graph still has characteristic "humps" where the bits with high
probability in the original characters making up the hash code
don't get enough chance to interact with more randomly
distributed bits. (Although the "hump" does now span a width of 1 bit
rather than 2 in the original distribution.)
|
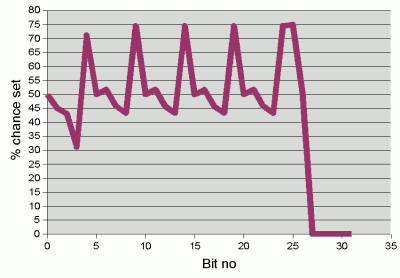
Probability of successive bits being set in the hash code
of a randomly-generated 5 character string, when 32 is chosen
as the multiplier in the hash function.
|
Improving the multiplier
Now we plot the same graph using 31 as the multiplier, as in the Java
implementation of the String hash code function. Multiplying
by 31 effectively means that we are shifting the hash by 5 places but
then subtracting the original unshifted value:
int hash = 0;
for (int i = 0; i < length(); i++) {
hash = (hash << 5) - hash + charAt(i);
}
return hash;
There are now further interaction among the bits. Firstly, adding
the ith character and subtracting the hash (with the previous
character in its lower bits) brings the per-bit probabilities in the character
closer to 50%. (For example, if we have two bits, each with a probability
of 70% of being set, then subtracting one from the other leaves a probability
of 42% that the resulting bit will be set, with a 21% chance of there being
a carry from the bit to the left.) And now, rather than just combining the
high bits of the ith number with the low bits of the previous
character, there are interactions generally between the lower bits of the nth
character and the higher bits of the n-1th character.
|
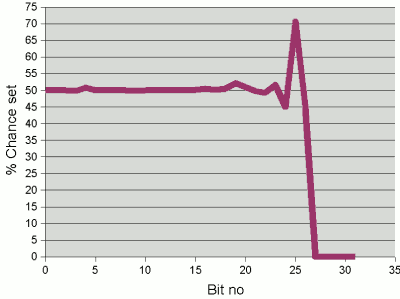
Probability of successive bits being set in the hash code
of a randomly-generated 5 character string, when 31 is chosen
as the multiplier in the hash function.
|
The result of these various points of interaction is a much flatter
bit distribution in the restulting hash code. With 5 character keys, the
profile is fairly flat up to bit 22, meaning that we can store a few million
such keys fairly efficiently.
Next...
Depending on your needs, here are some suggestions of what to read next:
1. It is occasionally given as a string hash function, e.g. in
Granet, V. (2004), Algorithmique et programmation en Java, Dunod, 2nd ed, p. 277,
but if suitable, this is only when the hash table has a prime number of
buckets (which the HashMap implementation no longer does).
If you enjoy this Java programming article, please share with friends and colleagues. Follow the author on Twitter for the latest news and rants.
Editorial page content written by Neil Coffey. Copyright © Javamex UK 2021. All rights reserved.