RSA key lengths
When you create an RSA key pair, you specify a key length in bits.
To set the RSA key length in Java, on during key pair generation, you call KeyPairGenerator.initialise():
KeyPairGenerator gen = KeyPairGenerator.getInstance("RSA");
gen.initialize(keyLength);
But what RSA key length should you choose? Here are some guidelines on RSA key length, with further discussion below:
- unless you can accept a relatively low level of security and are running on modest hardware,
you should generally choose an RSA key length of at least 2048 bits (current NIST recommendation);
- if you are running on recent dedicated hardware and/or require good security, then consider
a key size of 4096 bits;
- you could consider higher key lengths, but the performance overhead increase almost exponentially with key length,
meaning in practice a doubling of key length makes decryption some 5 times slower on modern hardware;
- otherwise, if you require long-term high security, ensure that your system could be
reconfigured at a later date to use a higher key length.
As with other encryption schemes, the RSA key length has a bearing on the computational complexity of
key generation, encryption and decryption— and therefore on the security of the encryption.
In the specific case of RSA, the key length relates to the number of bits in the modulus,
whereas in a block cipher such as AES it will generally reflect the block size.
But the practical implication is similar: we must choose a key length that provides an appropriate
trade-off between the required level of security and desired performance.
RSA key length and performance
RSA encryption is more computationally expensive than typical symmetric ciphers such as AES.
The key generation and decryption operations in particular are relatively expensive
operations. This is mitigated by the fact that in typical use, only a small piece of data
(such as another encryption key) is encrypted using RSA as a prelude to switching to a more
efficient scheme for the remainder of the communication. But it is still enough of an overhead
that it needs to be considered.
By way of example, the graph below shows some timings recorded for RSA decryption with different key lengths
from 512 to 5120 bits. Of the three operations, decryption is generally of primary concern because
it must be performed on every communication/login attempt and is much slower than encryption (the calculation
involves raising the message data to a huge decryption exponent, whereas the encryption exponent is typically small).
The graph shows a comparison between RSA decryption performance on a 4GHz Intel i7 (2015) versus an Apple M1 (2020).
As you might expect, the newer M1 CPU shows an overall improvement over the i7, but the overall
scalability of choosing higher key lengths remains similar.
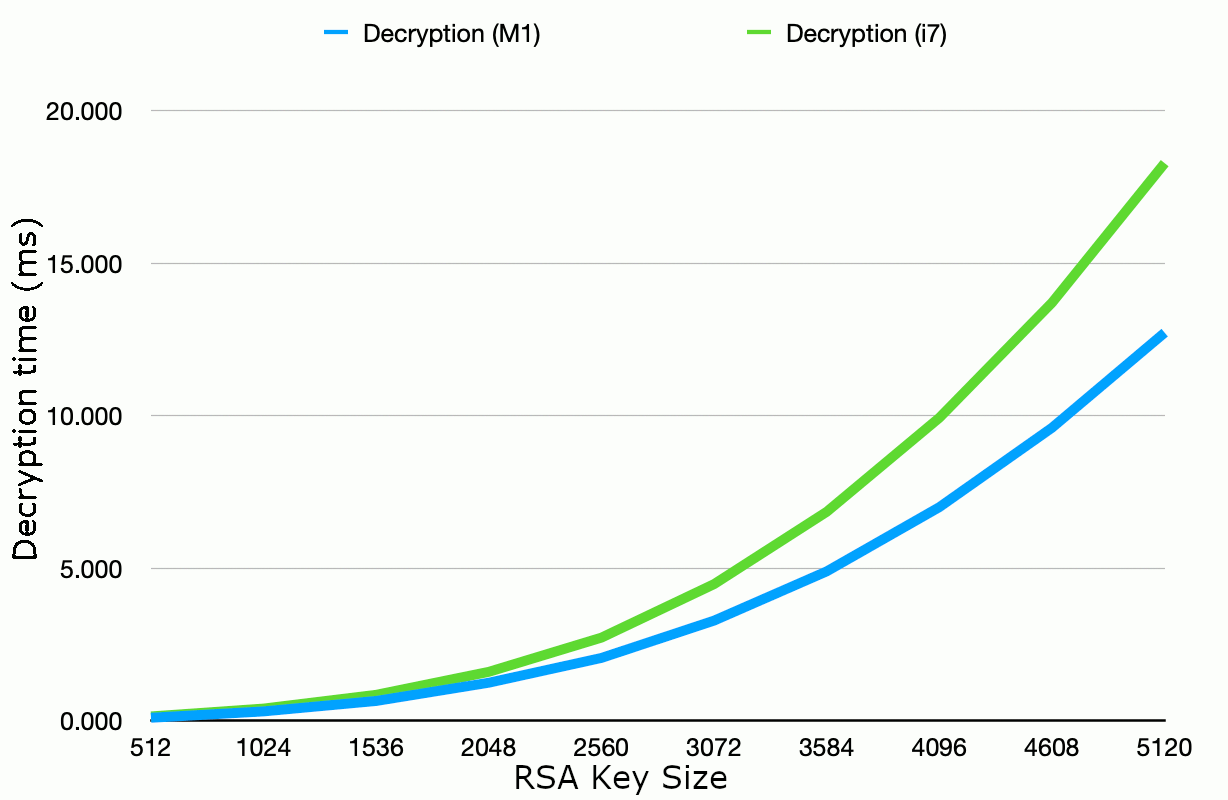
Figure 1: RSA decryption time by key length. Timings in milliseconds, JDK 11
running on a 4-core 4GHz Intel i7 vs an 8-core 3.2/2.0 GHz Apple M1.
As the graph shows, 2048-bit RSA decryption on modern hardware requires just a few milliseconds of CPU time
per decryption operatioon. This is likely to make 2048 bits a good choice in many cases where typical
levels of security are required. In many cases, you may consider that you can afford to increase this
fivefold in order to use 4096 bit keys. If you do so, bear in mind that e.g. for a login system,
this is the decryption overhead per attempt, not per successful login.
The performance of key pair generation is often a secondary consideration where key pairs are generated
once per server rather than once per session. However, in applications where you need to generate new key
pairs frequently, then generation time will be a concern. The graph below shows RSA key pair
generation time for differrnt key legths, again on a 4GHz Intel i7 versus Apple M1 for comparison:
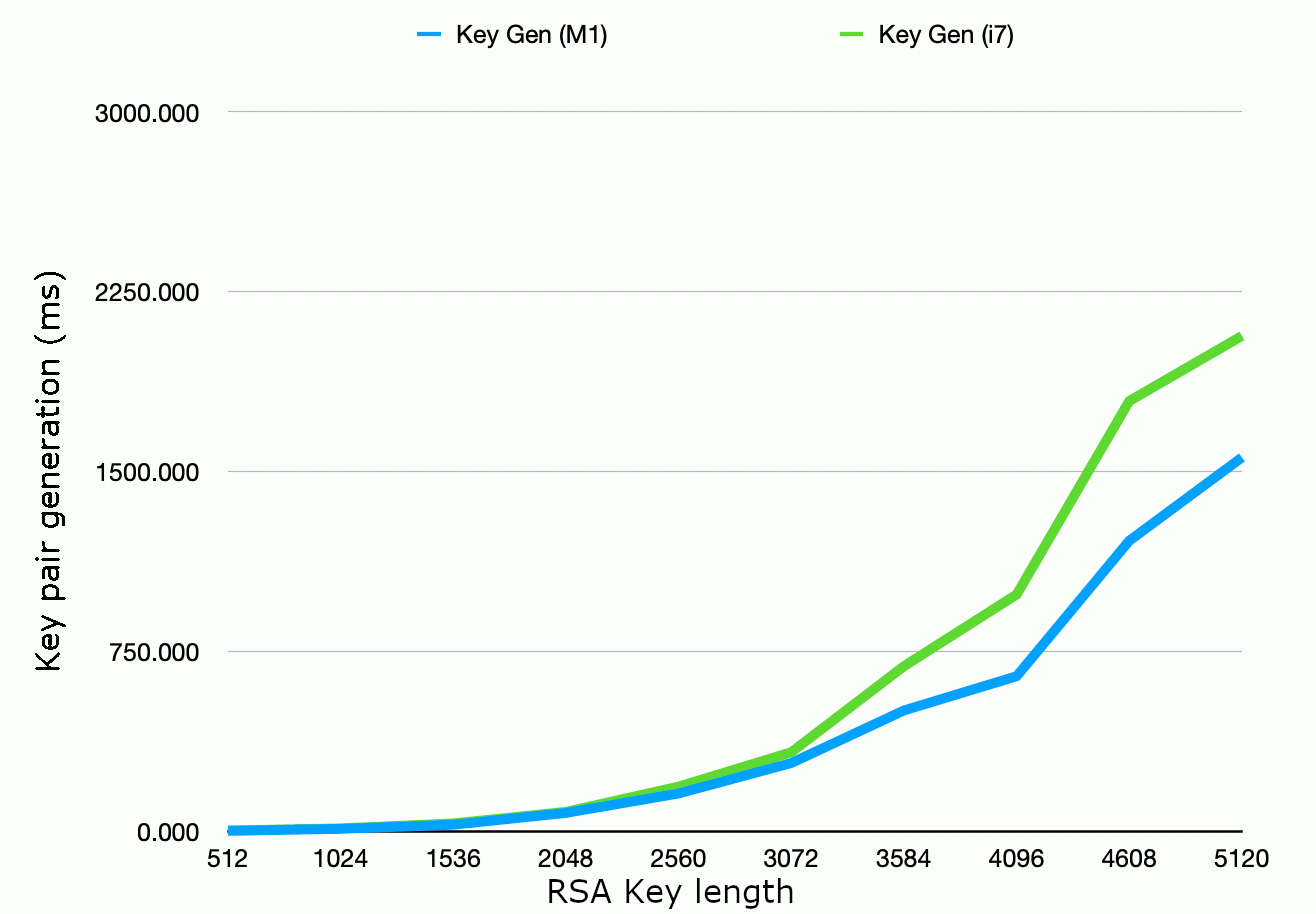
Figure 2: RSA key pair generation time by key length. Timings in milliseconds, JDK 11
running on a 4-core 4GHz Intel i7 vs an 8-core 3.2/2.0 GHz Apple M1.
Note that on both the i7 and the M1, a key length of 4096 bits appears to represent a "sweet spot" in
calculation time compared to the key lengths above and below. (N.B. Each data point in the graph above
is the average of 50 repetitions at the given key length, with the order of successive key lengths
randomised.) This may be because the security library
contains specific optimisations for this key length, and that is also something to consider.
How secure is (say) a 2048-bit RSA key?
The security of the RSA algorithm relies on the difficulty
of factoring a large number into the two prime numbers (used to generate the modulus)
that were originally multiplied together to form it. If an efficient algorithm came to light that could solve
this problem, then it would definitely break the security of RSA. There is a small risk that other techniques may
come to light that mean RSA is breakable without actually needing to factor the modulus. But as of the year 2020,
such cases are restricted to specific instances where the RSA algorithm is used "naively" in a way that
leaks information about the keys that it shouldn't do if used properly. Provided we stick to the standard
Java APIs and accompanying guidance when performing encryption, the question is essentially: can
a modulus of a given number of bits be factored by "brute force"?
Previous RSA key length recommendations have assumed that special hardware would be required to crack larger key
lengths. Shamir & Tromer (2003)
in their hypothetical TWIRL device,
suggested that for "a few dozen million US dollars", a hardware device could
be built to break a 1024-bit RSA key; Franke et al (2005) made a similar estimate.
Shamir & Tromer considered hardware because they estimated that a solution in software
would not scale beyond around 500 bits.
Based on these estimates,
Kaliski (2003)— see reference below— recommended the following RSA key lengths depending on the required
lifetime of confidentiality:
| Lifetime of data | RSA key size |
| Up to 2010 | 1024 bits |
| Up to 2030 | 2048 bits |
| Up to 2031 onwards | 3072 bits |
Recommended RSA key sizes depending on lifetime of confidential data.
Other authors have been more conservative. Ferguson & Schneier (2003) in Practical Cryptography implied that 2048 bits
would only be sufficient to keep data confidential for around 20 years, and were already recommending 4096 bit keys:
"The absolute minimum size for n is 2048 bits or so if you want to protect your data for 20 years.
[...] If you can afford it in your application, let n be 4096 bits long, or as close
to this size as you can get it." (p. 233)
As of 2020, how secure is a 2048 bit key length? One key observation is that, despite Shamir & Tromer's projection,
higher key lengths are being factored in software, albeit with steady progress rather than any sudden breakthrough so far.
One point of reference is the
RSA Factoring Challenge. This gives us an indication
of current capability by published means, biased towards the resources available to academic researchers.
Within that context, the largest RSA key to have been publicly factored is 829 bits (as of February 2020).
The graph below shows some of the gradual progress that has been made over the years from these competition results:
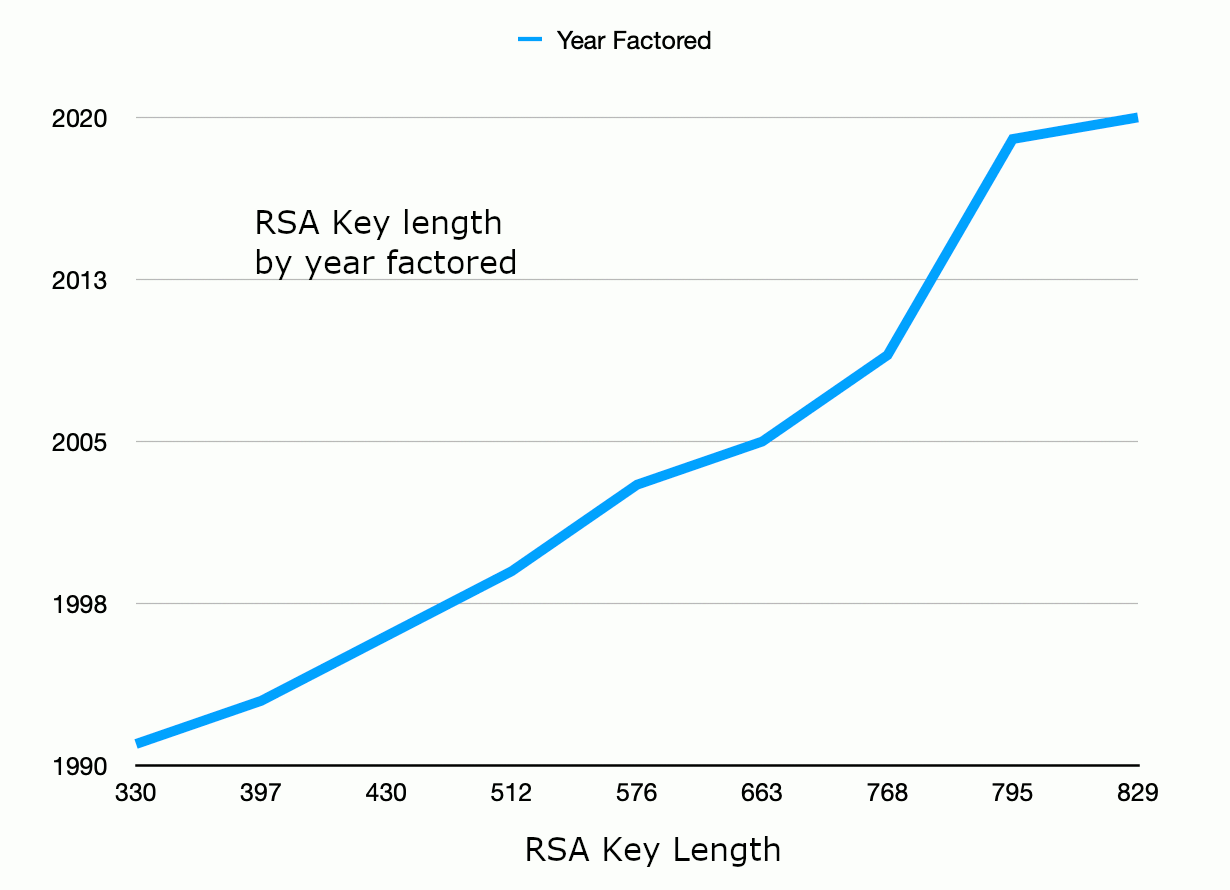
Figure 3: Progress in RSA factoring.
The factoring of RSA-250 (the 829 bit key) in 2020 required computing resources pooled across 6 research
institutions amounting to 2700 2GHz core-years of CPU time. From one perspective, this is around
1 million dollars of rented CPU time on a typical cloud service, or the equivalent of 100+ 8-core M1 processors running flat out for a year.
To a criminal who prefers not to pay for their computing time, this is potentially a few days of computing time on a botnet of 50,000 phones*.
This suggests that the 2009 estimate of Thorsten Kleinjung (one of the team that broke the 768-bit RSA-232 in 2009)— that around 8.4 million CPU years
would be needed to factor a 1024-bit
number in software3— may have been a little high.
We might consider that breaking RSA encryption with a key length of 1024 bits will soon represent
a feasible, targeted attack by a determined attacker (and may already be so for a state-sponsored attacker).
Therefore, a 2048-bit key length would seem to be an absolute minimum if you want to maintain a modest degree of security in the near term.
On the other hand, a 2048-bit key is not about to be attacked imminently if this is the maximum that your current hardware constraints
will allow.
Given the performance improvements in RSA key generatiomn and decryption observed between current hardware and that of a few
years ago, you can probably budget for a 4096-bit key on recent hardware.
Further reading
You may be interested in the following:
1. RSA recommend 1024-bit keys for "enterprise keys"
and 2048-bit keys for "root keys" (used for signing). See,
for example, Kaliski, B. (2003), TWIRL and RSA Key size.
2. Franke, J. et al (2005), SHARK: A Realizable Special Hardware Sieving Device for Factoring 1024-Bit Integers in Cryptographic Hardware and Embedded Systems � CHES 2005, Springer.
3. See Kleinjung, T. Estimates for factoring 1024-bit integers
4. In 2009, I speculated on an attack involving "several thousand 256-core machines (bearing in mind that that could be a fairly modest botnet by, say, 2020)".
What I of course underestimated is that, rather than an explosion in the number of cores in the average computer CPU, what we would see would be an
explosion in the number of 2- or 4-core CPUs in other devices in our day-to-day lives.
If you enjoy this Java programming article, please share with friends and colleagues. Follow the author on Twitter for the latest news and rants.
Editorial page content written by Neil Coffey. Copyright © Javamex UK 2021. All rights reserved.