Java tutorials home  Java cryptography  Encryption intro  Keys  Symmetric encryption  AES/block ciphers  Block modes (ECB, CTR, OFB)  Asymmetric encryption  RSA in Java  Comparison of algorithms  Key sizes  Hash functions

Search this site:

Secure hash functions in Java (ctd)

Now we've seen an introduction to hash functions, let's look at how to compute a hash in Java. As mentioned, secure hashes are sometimes called message digests. And in fact, the main class for computing them in Java is java.security.MessageDigest. We get an instance of MessageDigest, feed it an array (or several arrays) of bytes, then call its digest() method to get the resulting hash:

byte[] data = ....

MessageDigest md = MessageDigest.getInstance("SHA-1");
md.update(data);
byte[] hash = md.digest();

If we want to check that a given hash we're sent matches one we've just calculated, then we can use the MessageDigest.isEqual() method, passing in the two byte arrays representing the hashes (we could also use Arrays.equals()— it really is just a byte-by-byte comparison!).

In principle, you can see that the MessageDigest class has a similar pluggable architecture to the Cipher class: we pass in the name of the algorithm we want to use, and the security architecture finds a suitable provider that can fulfil that request. In practice, Sun's JDK ships with only a handful of hashes: MD2, MD5 and several SHA variants (SHA-1, SHA-256, SHA-384 and SHA-512). In fairness, there aren't currently many other choices in any case.

If you're just looking for the answer to the question which hash function should I use in Java? without too much philosophy, then the answer will almost certainly be SHA-256. Below we'll give some background as to why.

Performance of hash algorithms

Figure 1 shows the relative performance of these different hash algorithms. As we'll discuss below, to some extent, there's a tradeoff between security and performance, although it turns out that the more secure hashes are in fact "fast enough" for most applications.

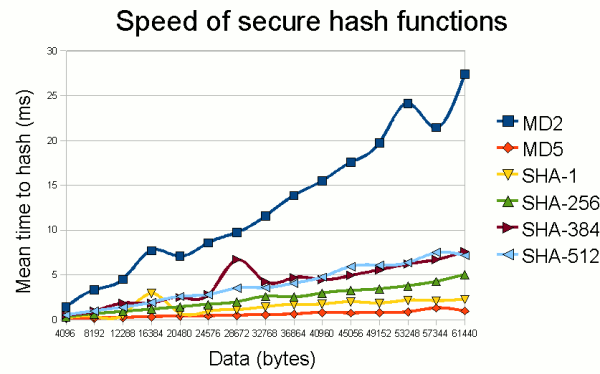
Figure 1: Performance of standard secure hash functions.
(Timings from a 2GHz Pentium running Java 6 under Windows XP;
each point is actually the mean of 20 measurements.)

As can be seen, the only hash algorithm (of those available by standard in Java) that really stands out from the rest is MD2. The fact that it is orders of magnitude slower than other hash functions will usually put it out of the running given that it is only 128 bits in width (see below), now considered unsuitable for any application where true security is required.

Other characteristics

In the following table, we summarise some more general characteristics of the various hash algorithms available by standard in Java.

MD2

MD2 is one of the earliest hash functions developed by Ron Rivest at RSA Security. To date, no full attack on MD2 has been published, but attacks have been published on the compression function (one of the components of the hash algorithm). Aside from this partial attack, the main reason for avoiding MD2 is that it is extremely slow compared to other algorithms (see Figure 1).

It is a 128-bit hash, meaning that we would expect to find a collision by chance after hashing 2⁶⁴ sets of data. Many consider this unacceptably low for new applications, considering they may need to cope with the volumes of data that people will be working with several years into the future.

Unfortunately, it is now considered insecure. Aside from the relatively small hash size, there are well-published methods to find collisions analytically in a trivial amount of time. For example, Vlastimil Klima has published a C program to find MD5 collisions in around 30 seconds on an average PC. If you need security, don't use MD5!

Although insecure, MD5 still makes a good general strong hash function due to its speed. In non-security applications such as finding duplicate files on a hard disk (where you're not trying to protect against the threat model of somebody deliberately fooling your system), MD5 makes a good choice.

SHA algorithms

SHA (Secure Hash Algorithm) refers collectively to various hash functions developed by the US National Security Agency (NSA). The various algorithms are based on differing hash sizes and (in principle) offer corresponding levels of security:

Conclusion

The above performance combined with the general security characteristics mentioned above mean that in practice, most applications will use SHA-256. It is really the only algorithm with sensible performance while still being secure at present.

The fact that there are now few viable hashing algorithms, and the most viable already has partial attacks, has made NIST sit up and take notice. They are running a public hash algorithm competition (similar to that which chose AES as the encryption standard) to chose the third generation of Secure Hash Algorithm (SHA-3). In 2011, the competition is now in its third round, consisting of a year dedicated to "public comment" of the 5 shortlisted finalists. The winner is to be chosen in 2012.

Update October 2012: The SHA-3 winner has now been chosen. This page will be updated shortly with more information.

1. See NIST (2006), NIST Comments on Cryptanalytic Attacks on SHA-1.
2. Sanadhya, S. K. & Sarkar, P. (2008), New Collision Attacks against Up to 24-Step SHA-2 in Progress in Cryptology - INDOCRYPT 2008, Springer.

Written by Neil Coffey. Copyright © Javamex UK 2012. All rights reserved.