Performance of the BigDecimal/BigInteger multiply() method (and potential improvement)

In our overview of BigDecimal and BigInteger arithmetic methods and their performance, we mentioned that the multiply() method scaled exponentially, specifically that multiplying an n-digit number by a m-digit number took within the order of nm time. It may have occurred to those who know a little about numerical algorithms that in fact algorithms exist for multiplying numbers which scale better than this.

The standard JDK implementation of the BigInteger (and hence BigDecimal) multiply() method uses the "naive" algorithm that effectively cycles through every combination of digits to multiply them together: essentially the same method that you would use if working out a multiplication with pencil and paper. A common, more efficient algorithm is one known as Karatsuba's method. This method breaks the problem down into a number of small multiplications (plus extra shifts and additions), and gains efficiency because it replaces every four multiplications with three. You may therefore be wondering why the standard JDK implementation doesn't use such a method, or at what point it is actually beneficial.

As I show below, it turns out that:

The JDK implementers presumably took the view that this was within a "typical" range. Beyond a few thousand digits, the more scalable Karatsuba method overtakes the performance. So if you have a specific need to multiply very large numbers quickly, you may be interested in implementing the Karatsuba algorithm (or other related algorithms).

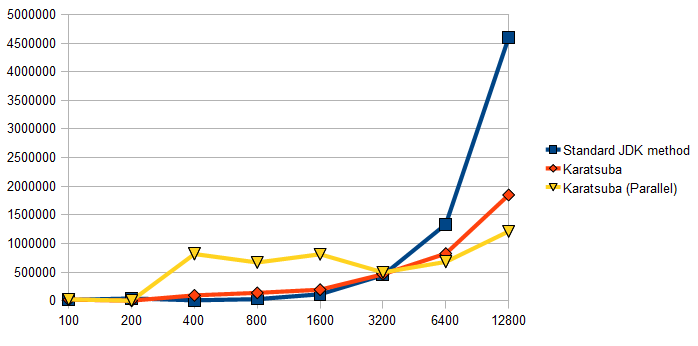
Figure 1: Timing of multiplication of two BigIntegers using the standard "naive" JDK algorithm, an implementation of Karatsuba's algorithm and a version of this algorithm that parallelises the three multiplications in each iteration. Timings made on a (4-core hyperthreading) Intel i7 machine in Hotspot version 1.7.0.

Figure 1 above shows the performance of multiplication of pairs of n-digit numbers using the standard JDK multiply() method, alongside timings with an implementation of Karatsuba's algorithm. (Notice that the horizontal scale is logarithmic: each graduation marks a doubling of the magnitude of the numbers.) As can be seen, although Karatsuba's method is more efficient in principle, in practice it only becomes beneficial when the numbers being multiplied reach an order of around 3,000 digits. This happens because the naive method, although inefficient in how it scales, has little overhead: it consists essentially of a nested compact loop without method calls.

Parallelisation

A challenge for modern programming is the trend for new performance innovations of processors to involve increased parallelism rather than increased core speed. A potential advantage of Karatsuba's algorithm it permits a simple means of parallelisation: the three multiplications of each "round" can be run in parallel on separate cores.

I therefore also took timings for a simple parallelised implementation of Karatsuba's algorithm as described. Again, with numbers of small magnitude, the overhead of parallelisation clearly outweighs any potential benefit. Only when the numbers reach a magnitude of around 6,000 digits does the parallel algorithm show a benefit over the non-parallel Karatsuba implementation. With this simplistic form parallelisation, the parallel version gave a tangible benefit, although was only around twice as fast as the non-parallel version.

---